この前、適当に数学の過去問を貪っていると、かなり面白そうな問題に出会いました。

2013年度 東京大学前期試験 理系数学の第5問です。(画像は河合塾から拝借。一部加工。)
今回はこの問題(小問2)を誘導に乗らず様々な解法で解いてみたいと思います。
問題文は長いですが、問うている内容は至極シンプル。しかしながら証明は難しいと。さらに証明までの道のりが多様に存在しそうに見えるのもあり、フェルマーの最終定理のように、挑戦してみようという意欲が湧きやすい良問だと思います。
とはいえ一問辺り30分弱しか与えられない入試においては証明まで辿り着くのは厳しく、誘導が下手(個人の見解)なのもあり入試問題としてはかなり難問。僕も時間内では全く糸口が掴めなかった。入試には向かない問題と言えるでしょう。誘導の仕方も含め、ある意味東大らしいとは思いますが。
また、河合塾の模範解答は以下になります。誘導に乗る解き方はこちら。
http://kaisoku.kawai-juku.ac.jp/nyushi/honshi/13/t01-21a/9.html
さて、早速証明に取り掛かってみましょう。命題Pは自明とまではいかなくとも、n(n+1)(n+2)で表せる数は無限にあるのだし、nを大きくしていけばいつかは見つかりそうだと直感的には思うでしょう。
しかし、いざ証明しようとすると、雲を掴むようで一歩目すら踏み出せない。そこでまずは三つの連続する自然数の積について言えること、また何をすれば証明となるかを書き出してみます。
その前に定義を。
- 一般項が a_n = (n-1)n(n+1) である数列a_nを定義する。(n≧2)
まず、a_nについて言えることは、
- a_n は常に6の倍数である。・・・①
- a_n = n³ - n と展開できる。・・・②
- a_(n+1) - a_n = n(n+1)(n+2) - (n-1)n(n+1) = 3n(n+1) ・・・③
- a_(n+1) / a_n = (n+2) / (n-1) = 1 + 3 / (n-1) ・・・④
あたりでしょうか。一方、証明の形としては、
- ある特定のn=Nにて、a_Nが条件(b)を満たすと示す。・・・⑤
- nがある条件Qを満たすとき、a_nは条件(b)を満たし、Qを満たすnが存在することを示す。・・・⑥
- 1がm回連続現れるa_nが存在すると仮定すると、1がm+1回連続現れるa_nが必ず存在すると示す。(数学的帰納法)・・・⑦
くらい。⑤は厳密には⑥に包括されますが、分かりやすくするため分割しました。
準備立ては出来たので、次に作戦を考えます。始点(①~④)から攻める解き方と、終点(⑤~⑦)から攻める解き方がありますが、まずは①~④を詳しく掘り下げながらそれぞれが⑤~⑦のどの形に使えそうかを模索していくことにしましょう。
①について。これは簡単に思いつきますが、6の倍数だからといってどうということもなく、発展させにくい。
②について。これはかなり有用に見えます。というのも、n³とnでは桁数に大きく差が開き、nに巨大な数を入れると片方がほぼ無視できるからです。nを無視するのは勿論、後述する手段をとればn³も無視できます。n³ - nに1が99回連続で現れると示すのは難解でも、n³やnに現れるのを示すのはいくらか楽でしょう。
③、④について。これらはa_nの増加具合を差と商の二つの側面から関数としたものです。③を見るとa_nは加速度的に大きくなっていくように見えますが、④を見るとa_nとa_n+1の比率はnが大きくなるほど1:1に近づき、変化の大きさは穏やかになると読み取れます。例えばa_3はa_2の4倍ですが、a_10000はa_9999のたった1.0003倍にしかなりません。nが大きくなるにつれa_nの変化がゆっくりになるのであれば、そこに糸口が見つかるかもしれません。
②から証明してみましょう。これは⑤に行き着きそうな道筋です。
まずはnを無視する方法。n³ - nについて、nがm桁だとすると、n³は3m桁くらいあり、m+1桁目から3m桁までの数字は殆ど変わりません。

上の例では、青線より左の8桁でn³とn³ - nの数字が完全一致しています。
このことを証明に用いてみましょう。上から99桁が全て1となるn³があることを示し、その部分はnを引いても変わらないことを示せば証明完了ですね。(ただしこのnを引いても変わらない、というのを示すのが厄介で、少し遠回りをすることになります。)
証明1
111111...(中略)...1111 と1が100個続く数をXとおく。
³√X < ³√(X+1)である。よって、自然数mが十分大きいならば、
10^m * ³√(X+1) - 10^m * ³√X > 1 という式が成立する。
mがこの式を満たす時、10^m * ³√(X+1) と 10^m * ³√X の間には必ず自然数が存在するはず。この自然数をNとおく。
10^m * ³√X < N <10^m * ³√(X+1) 両辺を3乗して、
X * 10^3m < N³ < (X+1) * 10^3m となる。・・・(ⅰ)
X = 1111111...111(1が100個)、X+1 = 111111...112(1が99個と2が1個)なので、N³の上から100桁は全て1である。
また、mがある閾値より大きければ、10^3m > N という式が成立する(証明割愛)。
(ⅰ)不等式の左部分と10^3m > Nより、
(X-1) * 10^3m < N³ - N という式が作れる。
また、(ⅰ)の右部分よりN³ - N < (X+1) * 10^3m という式も作れる。
(X-1) * 10^3m , (X+1) * 10^3m は桁数が同じで、共に上から99桁は全て1なので、その間に位置するN³ - Nも上から99桁が全て1である。
よって、(N-1)N(N+1)が条件(a),(b)を満たす自然数として存在する。(証明終)
終わってみると⑤ではなく⑥に行き着いてしまいました。ともかくこれでひとまず示せましたね。しかし後半部分が強引で汚いため、理解しづらいものになってしまいました。もう少し綺麗に示したいですね。
ここで、この証明の次の部分に注目してみます。
- 自然数mが十分大きいならば、10^m * ³√(X+1) - 10^m * ³√X > 1 という式が成立する。
これを少し改変すれば、「自然数mが十分大きいならば、10^m * ³√(X+1) - 10^m * ³√X > 3 という式が成立する」とも言えます。つまり、このとき 10^m * ³√(X+1) と 10^m * ³√Xの間には3つの自然数が入ることになりますね。
一方、a_n=(n-1)n(n+1)であることより、(n-1)³ < a_n < (n+1)³が 導けます。
この二つを使えばもっとすっきりした証明が出来そうですね、やってみましょう。
証明2
(途中までは証明1と同じ)
自然数mが十分大きいならば、10^m * ³√(X+1) - 10^m * ³√X > 3 という式が成立する。
mがこの式を満たす時、10^m * ³√(X+1) と 10^m * ³√X の間には必ず自然数が3つ存在するはず。この自然数をN-1,N,N+1とおく。
10^m * ³√X < N-1 < N+1 <10^m * ³√(X+1) それぞれ3乗して、
X * 10^3m < (N-1)³ < (N+1)³ < (X+1) * 10^3m
一方、a_nの定義より、(N-1)³ < (N-1)N(N+1) < (N+1)³。
これらを組み合わせると、
X * 10^3m < (N-1)N(N+1) < (X+1) * 10^3m という式が成立する。
よって(N-1)N(N+1)の初めの100桁は全て1である。
以上より、(N-1)N(N+1)が条件(a),(b)を満たす自然数として存在する。(証明終)
長さとしては証明1と変わりませんが、幾ばくか理解しやすくなったように思います。答案用紙に書くなら証明1でやろうとしていても途中で証明2にルート変更したいですね。
次はn³のほうを無視する方法。
n = M * 10^m と表したとき(Mは自然数)、mが十分大きければn³ - nの計算が一部非常に簡単になります。説明しても分かりづらいので、証明を先に記してみます。
証明3
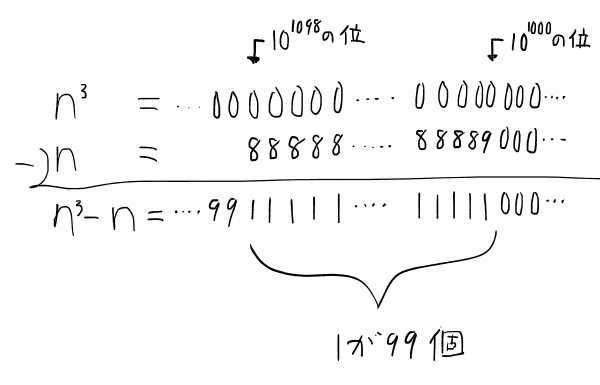
Y = 88888888...(中略)...88889 (8が98個続き、9が1個) とする。
n = Y * 10^1000のとき、nは1099桁の数である。
一方、n³ = Y³ * 10^3000なので、n³は下から3000桁目までは0が続く。
よって、n³ - nを計算すると、
となり、n³-n = (n-1)n(n+1) には1が99個連続で現れる箇所がある。
よって、n = Y * 10^1000 のときの(n-1)n(n+1)が(a),(b)を共に満たす自然数として存在する。(証明終)
n = M * 10^m と表したとき、mが十分大きければn³に多くの0が発生し、n³ - nの結果が一部とはいえ楽になります。あとはn³ - nに1が99回連続で発生するようにMに適当な値を代入すれば良いだけです。
あんな難問に見えた問題がこんな簡単に示せるとは意外ですね。手前味噌ですが先ほどの証明よりだいぶシンプルで美しい証明だと思います。
③、④から、証明してみましょう。③、④について一度再確認してみましょう。
- a_(n+1) - a_n = n(n+1)(n+2) - (n-1)n(n+1) = 3n(n+1) ・・・③
- a_(n+1) / a_n = (n+2) / (n-1) = 1 + 3 / (n-1) ・・・④
④より、a_(n+1)とa_nの比率はnが大きくなれば徐々に1に近づくと分かります。
つまり、増加率はどんどん下がっていくため、nが十分大きい時にはa_nの上から99桁の数はゆっくりとしか変わっていかないことになります。それならば、11111...(中略)...11110で始まるa_nと11111...(中略)...11112で始まるa_nの間に11111...(中略)...11111で始まるa_nがあると言えそうです。やってみましょう。
証明4
一般項が a_n = (n-1)n(n+1) である数列a_nを定義する。(n≧2)
また、111111...(中略)...1111 と1が99個続く数をXとおく。
定義より、a_(n+1) / a_n = (n+2) / (n-1)
= 1 + 3/(n-1)
1 + 3/(n-1)はnが大きくなるほど小さくなり、n→∞で1 + 3/(n-1) = 1なので
nがある数より大きければ、
(n+2) / (n-1) < (X+1) / X という不等式を満たせることが分かる。
また、a_(n+1) / a_n = (n+2) / (n-1) でもあるので、nが十分大きいとき、
a_(n+1) / a_n < (X+1) / X である。(ⅰ)
(ⅰ)式を満たすnの一つをNとする。
ここで自然数kを定義する。kはa_N < X * 10 ^ k という不等式を満たすとする。
また、a_nは単調増加かつn→∞で∞に発散するので、
a_n ≦ X * 10 ^ k < a_(n+1)を満たすnが一つのみ存在するはず。(ⅱ)
このnをMとおく。M ≧ Nなので、Mは(ⅰ)式を満たす。
ここで、(ⅰ),(ⅱ)から、
a_(M+1) / a_M < (X+1) / X
a_M ≦ X * 10 ^ k の二式が言える。
この二式を辺々かけて、
a_(M+1) < (X+1) * 10 ^ k となる。
さらに(ⅱ)の右部分より、
X * 10 ^ k < a_(M+1) であるので、組み合わせて
X * 10 ^ k < a_(M+1) < (X+1) * 10 ^ k
よって、a_(M+1)の上から99桁は全て1である。
以上より、a_(M+1) = M(M+1)(M+2) が(a),(b)を満たす自然数として存在する。(証明終)
nが大きくなるとa_nの上部は殆ど変わらなくなる。それならいずれ上から99桁が殆ど変わらなくなることもあるという訳ですね。
③からも同じような方法で示せますが、この証明との違いは殆ど無いので割愛します。
次は証明結果(⑤~⑦)をイメージして、そこから①~④の性質が関連しない証明方法を探してみます。
- ある特定のn=Nにて、a_Nが条件(b)を満たすと示す。・・・⑤
- nがある条件Qを満たすとき、a_nは条件(b)を満たし、Qを満たすnが存在することを示す。・・・⑥
- 1がm回連続現れるa_nが存在すると仮定すると、1がm+1回連続現れるa_nが必ず存在すると示す。(数学的帰納法)・・・⑦
⑥は漠然としすぎててスタートラインにはしづらい。というわけで⑤か⑦でしょう。
⑤で始めてみましょう。
1が99回出てくるような(n+1)n(n-1)を探せばいいのですが、証明1の辺りで述べたとおり、これを探し出すのは至難の業です。
ここで、これまでの証明でも活躍した10の累乗に登場してもらいます。彼ならこの問題を解決してくれるかもしれません。
証明3とは趣向を変え、n = 10^1000 + M と置いてみます。
このとき、(n+1)n(n-1) = (10^1000 + M + 1)(10^1000 + M)(10^1000 + M - 1)
= 10^3000 + 3M * 10^2000 + 3M² * 10^1000 + M³ - M
ここで、1が99個続く部分を最も作り易そうな項は3M * 10^2000でしょう。Mに適当な値を入れれば容易に3Mという数の中に1が99回連続で出てくるように出来ます。
実は、この証明方法は誘導と同じ発想だと思われます。小問1の唐突な不等式はこうして導かれたんですね。これ以下の証明は模範解答と全く同じとなります。
また、3M² * 10^1000の項でも1が連続に出てくるように出来ますが、3M²に1が99回連続で現れるMを強引に見つけるという、証明1とかなり似通った証明となるのでこちらも割愛します。
残りは⑦です。数学的帰納法は発想としてもすぐに浮かぶ物ではないですし、このような証明に帰納法が使えるかも未知数ですがとりあえずやってみましょう。
感覚的には、1が少なくともm個連続で並んでいるa_nがいくつもあったら、その内15%~20%位は1がm+1個以上並んでいるa_nになりそうです。その計算だと、0.15^99程度の確率(1無量大数 分の1よりも起こりづらい確率!)ではありますが、条件(b)を満たすa_nは存在します。
ですが、a_nに1がm個以上連続で現れるときの、a_nに1がm+1個以上連続で現れる条件付き確率を算出することは現実的ではないので、別の方法を探しましょう。
他には、この様な方法が考えられます。1がm個連続で並ぶa_nが一つ見つかった時、そのnに適当な処置をすれば、1がm個以上連続で並ぶ別のa_nが見つかるなどとすれば、1がm+1個連続で並ぶa_nも見つかるかもしれません。しかし、こちらも色々探しましたが見つかりませんでした。その”適切な処置”が見つからないのです。例えばnを十倍すると、a_10nはa_nの大体1000倍になりますが、a_10nにも必ず1がm個並ぶとは言いきれません。③、④を使って、nを一つずつずらしていくというのは使えますが、結局証明4を遠回りして示すような証明になるので没です。
そんなわけで、色々考えてみましたが数学的帰納法では効果的なアプローチが見つかりませんでした。あと一歩って気がするんですけどねえ。
以上、4通り(割愛した分も含めると7通り)で示してみました。高校範囲ではこれが限界ではないでしょうか。数学的帰納法の可能性は残されてますが。難問に見えましたが意外と証明への道筋が多いのは面白いように思います。
因みに、別に1が99個でなくとも、任意の数の並びが含まれるa_nは存在します。証明内でX(もしくはY)を適当な値に置き換えれば証明可能です。
おまけになりますが、(b)の条件には「10進法で表したとき」とあります。この10進法という条件がなければ、
証明5
以下、2進法で記す。
n = 10 ^ 110010 (10進法に直すと2^50)のとき、
(n-1)n(n+1) = (10^110010 - 1)(10^110010)(10^110010 + 1)
= 10^10010110 - 10^110010 (10進法に直すと2^150 - 2^50)
と、この数は1が100個連続(10進法表記)で現れる数である。
よってこのとき(a),(b)を共に満たす。(証明終)
証明6
以下、28進法で記す。
n = 10 ^ 3G (10進法に直すと28^100)とおく。このとき、
(n-1)n(n+1) = n³ - n
= RRRRRRR...(中略)...RRRR000...(中略)... (Rが10進法表記で200回続き、0が同じく100回続く)
である。(Rは10進法表記で27。)
ここで、(n-1)/3と(n-1)/3 + 1と(n-1)/3 + 2の積について考える((n-1)/3は整数。)
これらの積は (n-1)(n+2)(n+5)/R
=(n³+6n²+3n-A)/Rである。
これは{(n-1)n(n+1) + 6n²+4n-A}/Rと書き換えられる。
(n-1)n(n+1)/Rは1が10進法表記で200回続き、0が同じく100回続く数である。
また、(6n²+4n-A)/Rは10進法表記で200桁の数である。
よって、(n-1)n(n+1)/Rと(6n²+4n-A)/Rの足し算で、10進法表記で下から200桁目で繰り上がりが起こったとしても、
(n-1)n(n+1)/R + (6n²+4n-A)/Rは10進法表記で上から99桁の間は1が続く。
以上より、(n-1)/3と(n-1)/3 + 1と(n-1)/3 + 2の積が(a),(b)を満たす。(証明終)
等といった証明も可能となります。手順としては簡潔ですが、2、28進数と10進数の間の翻訳の手間がかかるのでどっちにしろ面倒くさいですね。